pml-book1

2 : Probability: Univariate Models

2.2 Random Variables

• Basic
  • ... random variable (rv)
  • ... sample space / state space
• Discrete / Continuous
  • is discrete rv is finite/countably infinite
    • Probability mass fuction (pmf) :
  • is continuoius rv
    • Cumulative distribution fuction (cdf) :
    • Probability densitry function (pdf) :

2.2.2.3 Quantile / Quartiles

• Quantile : inverse cdf / percent point function (ppf)
  • q's quantile
• Quartiles
  • and are the lower / upper quartiles
  • 日本語では、四分位点(しぶんいてん)という。
• Example
  • ... cdf of Gaussian distribution
    • 
      is 95% interval.

2.2.3 joint distribution / 2.2.4 independence etc

• Joint distribution

• Conditional distribution

• product rule :

• (unconditionally) independence / marginally independence

• conditionally independence (CI)

2.2.5 Moments of a distribution

• mean / expected value
  • for discrete rv :
  • for continuous rv :
• variance (often denoted by )
  • standard deviation :
• The variance of product of independent rv:

2.2.5.4 Conditional moments

• law of iterated expectations / law of total expectation

• derivation

• Example : Lightbulb
  • Factory 1 supplies 60% bulbs, lifetime (hr)
  • Factory 2 supplies 40% bulbs, lifetime (hr)

2.2.6 Limitation of Summary Statistics

2.3 Bayes' rule

• Bayes' rule
  • For unknown (hidden) quantity
  • Given some observed data

• Details
  • ... Prior Distribution
  • ... Likelihood
  • ... Posterior Distribution
• Posterior Prior Likelihood

Example 1 : Testing for COVID-19

• Notation
  • : infection event (1=infected, 0=uninfected)
  • : diagnosis test result (1=positive, 0=negative)
• Aim
  • calc : infected probability when test positive
  • calc : infected probability when test negative
• Assumption (based on NYC situation in Spring 2020)
  • Likelihood
    • Sensitivity
    • Specificity
  • Prior (of infection) :

(Cont.)

• calc : infected probability when test positive

• calc : infected probability when test negative

Example 2 : The Monty Hall problem

• Game flow
  • There 3 doors : No.1, No.2, No.3
    • A single prize has been hidden behind one of theme.
  • At first, you choose a door (suppose door 1)
  • Gameshow host opens one of the other two doors (suppose door 3)
    • no prize behind it
  • You can change your choice (door 1 or door 2)
• Problem : Should you
  • (a) choose door 1 ?
  • (b) choose door 2 ?
  • (c) or no difference

(Cont.)

• Notation
  • : hypothesis that the prize is hidden behind door No
  • : Gameshow host opens door 2(,3)
• Assumption
  • Prior :
  • Likelihood

(Cont.)

• After observed , apply Bayes' rule

(Cont.)

• Finally:

• You sholud change your choice to door 2!

2.4 Bernoulli / Binomial distribution

• Bernoulli :
  • (ex) coin toss (1=head / 0=tail)
  • (ex) probability of head

• Binomial :
  • (ex) num of heads in -times coin toss

2.4.2 Sigmoid function

• Sigmoid function :
• Sigmoid function + Bernoulli
  • predict probability given some input

Logistic regression

• using linear predictor :

2.5 Categorical / Multinomial

• Categorical :

  • , where is num of categories
  • In other word :

• Multinomial :

  • is the number of occurreces of category

Softmax / Multiclass Logistic

• Softmax (or multinomial logit)

• Multiclass Logistic regression

  • Using

2.5.4 : Log-Sum-Exp trick

• Softmax :
  • "exp" value overflows on a computer when is big!
• Log-Sum-Exp trick : Use

• lse function

2.6 Univariate Gaussian (normal)

• Recall : cumulative distribution dunction ; cdf
• Gaussian distribution (cdf)

• using

(Cont.)

• Recall : probability density dunction ; pdf
• pdf of Gaussian

• moments
  • mean :
  • variance :

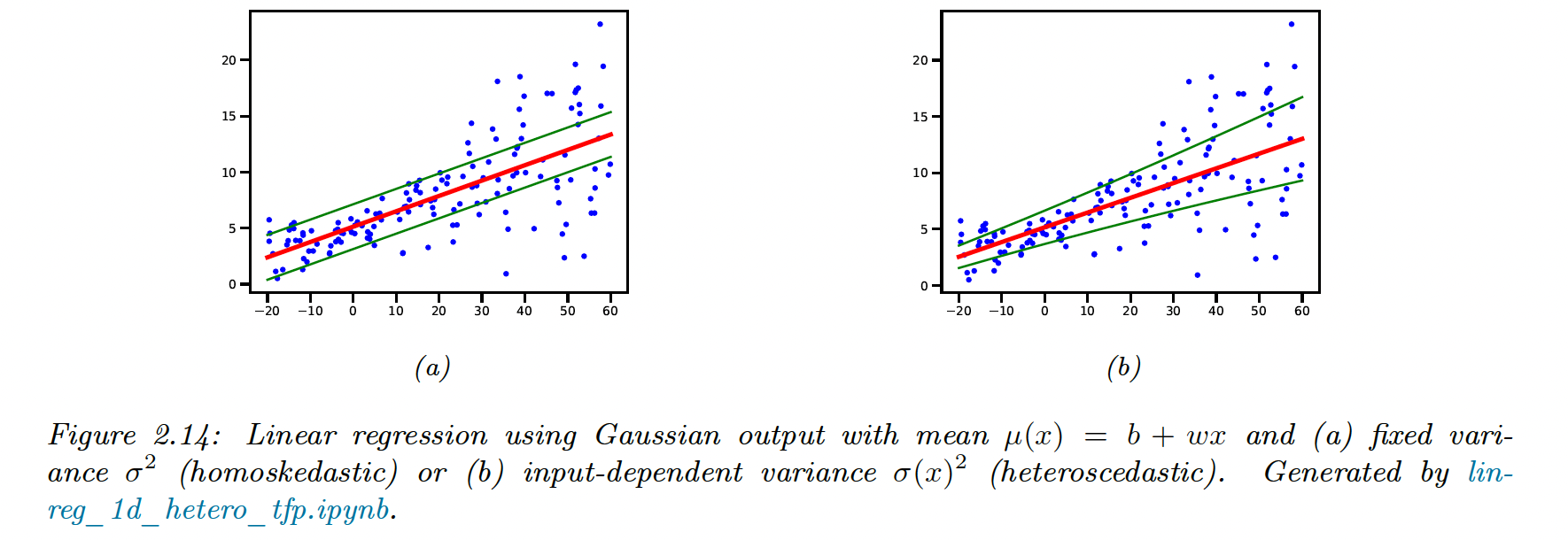
2.6.3 : Regression

• Normal distirbution conditioned on input variables :

• Homoscedastic regression (Linear regression)

• Heteroskedastic regression